数组
理论知识
- 数组下标都是从0开始的。
- 数组内存空间的地址是连续的
正是因为数组在内存空间的地址是连续的,所以我们在删除或者增添元素的时候,就难免要移动其他元素的地址。
二分查找
https://programmercarl.com/0704.%E4%BA%8C%E5%88%86%E6%9F%A5%E6%89%BE.html
https://leetcode.cn/problems/binary-search/
思路
明确好区间的定义,是左闭右闭即[left, right],还是左闭右开即[left, right)
方法一:左闭右闭即[left, right]
定义target在[left, right]区间,所以有如下两点:
- while (left <= right) 要使用 <= ,因为left == right是有意义的,所以使用 <=
- if (nums[middle] > target) right 要赋值为 middle - 1,因为当前这个nums[middle]一定不是target,那么接下来要查找的左区间结束下标位置就是 middle - 1
function search(nums: number[], target: number): number {
let left = 0
let right = nums.length - 1
while(left <= right){
let i = Math.floor((left + right) / 2)
if(nums[i] === target){
return i
}else{
if( nums[i] > target ){
right = i - 1
}else{
left = i + 1
}
}
}
return -1
};
Math.floor 而不是 Math.ceil如果使用 Math.ceil,在某些情况下,left 和 right 很靠近,mid 会更偏向右边,可能导致死循环。
举例:
- 如果
left = 1,right = 2floor((1 + 2)/2) = 1,下一步可能设置left = 2或right = 0,总能跳出循环;- 但
ceil((1 + 2)/2) = 2,如果逻辑不当,就会卡在left = 1, right = 2的循环中。
- 使用
Math.floor是为了避免死循环,让中间值偏向左边更稳定; - 使用
Math.ceil理论上也可,但需要更严格地处理边界,容易出错;
方法二:左闭右开即[left, right)
如果说定义 target 是在一个在左闭右开的区间里,也就是[left, right) ,那么二分法的边界处理方式则截然不同。
有如下两点:
- while (left < right),这里使用 < ,因为left == right在区间[left, right)是没有意义的
- if (nums[middle] > target) right 更新为 middle,因为当前nums[middle]不等于target,去左区间继续寻找,而寻找区间是左闭右开区间,所以right更新为middle,即:下一个查询区间不会去比较nums[middle]
function search(nums: number[], target: number): number {
let left = 0
let right = nums.length
while(left < right){
let i = Math.floor((left + right) / 2)
if(nums[i] === target){
return i
}else{
if( nums[i] > target ){
right = i
}else{
left = i + 1
}
}
}
return -1
};
这个相较于左闭右闭不好理解
- 首先是
let right = nums.length,因为定义target在左闭右开的区间里,即:[left, right) - while (left < right) , 因为left == right的时候,在[left, right)是无效的空间,所以使用 <
- right = middle,因为target 在左区间,在[left, middle)中
移除元素
https://programmercarl.com/0027.%E7%A7%BB%E9%99%A4%E5%85%83%E7%B4%A0.html
https://leetcode.cn/problems/remove-element/description/
思路
题目要求:需要原地移除
因为元素在内存地址中是连续的,不能单独删除数组中的某个元素,所以只能覆盖
暴力解法
暴力的解法就是两层for循环,一个for循环遍历数组元素 ,第二个for循环更新数组。
function removeElement(nums: number[], val: number): number {
let n = nums.length
for(let i = 0; i <n; i++){
if( nums[i] === val ){
for(let j = i+1; j<n; j++){
nums[j - 1] = nums[j]
}
i--
n--
}
}
return n
};
i--因为当前 i 位置又是新元素了,必须重新检查这个位置!所以 i--
双指针法
双指针法(快慢指针法): 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
定义快慢指针
- 快指针:寻找新数组的元素 ,新数组就是不含有目标元素的数组
- 慢指针:指向更新 新数组下标的位置
function removeElement(nums: number[], val: number): number {
let slowIndex = 0
for(let fastIndex = 0; fastIndex < nums.length; fastIndex++){
if(nums[fastIndex] !== val){
nums[slowIndex] = nums[fastIndex] // 保留有效值
slowIndex++
}
}
return slowIndex
};
其他解决方法
这种方式是我自己想到的,定义两个指针,一个从开头,一个从结尾开始交换
function removeElement(nums: number[], val: number): number {
let i = 0
let j = nums.length - 1
for(;i<=j;i++){
if(nums[i] === val){
nums[i] = nums[j]
j--
i-- // 这里的i为什么要--需要理解
}
}
return i
};
有序数的平方
https://programmercarl.com/0977.%E6%9C%89%E5%BA%8F%E6%95%B0%E7%BB%84%E7%9A%84%E5%B9%B3%E6%96%B9.html
https://leetcode.cn/problems/squares-of-a-sorted-array/description/
思路
暴力解法
先平方在排序
function sortedSquares(nums: number[]): number[] {
return nums.map(item => item * item).sort((a, b) => a - b)
};
双指针
数组其实是有序的, 只不过负数平方之后可能成为最大数了。
那么数组平方的最大值就在数组的两端,不是最左边就是最右边,不可能是中间。
此时可以考虑双指针法了,i指向起始位置,j指向终止位置。
function sortedSquares(nums: number[]): number[] {
let arr = []
let i = 0
let j = nums.length - 1
while(i <= j){
let a = nums[i] * nums[i]
let b = nums[j] * nums[j]
if( a >= b){
arr.unshift(a)
i++
}else{
arr.unshift(b)
j--
}
}
return arr
};
长度最小的子数组
https://leetcode.cn/problems/minimum-size-subarray-sum/description/
思路
暴力解法
暴力解法当然是 两个for循环,然后不断的寻找符合条件的子序列
function minSubArrayLen(target: number, nums: number[]): number {
let n = Infinity
for(let i= 0;i<nums.length;i++){
let s = 0
for(let j = i;j<nums.length;j++){
s += nums[j]
if(s >= target){
n = Math.min(n, j - i + 1)
break
}
}
}
return n === Infinity ? 0 : n
};
时间复杂度是O(n^2)
i - j + 1j 和 i 是你当前找到的子数组的起点和终点索引
比如子数组是从 nums[2] 到 nums[4],那么长度是多少?
- 索引
j = 4,i = 2 - 长度 =
4 - 2 + 1 = 3✅
滑动窗口
所谓滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果。
在暴力解法中,是一个for循环滑动窗口的起始位置,一个for循环为滑动窗口的终止位置,用两个for循环 完成了一个不断搜索区间的过程。
那么滑动窗口如何用一个for循环来完成这个操作呢。
首先要思考 如果用一个for循环,那么应该表示 滑动窗口的起始位置,还是终止位置。
如果只用一个for循环来表示 滑动窗口的起始位置,那么如何遍历剩下的终止位置?
此时难免再次陷入 暴力解法的怪圈。
所以 只用一个for循环,那么这个循环的索引,一定是表示 滑动窗口的终止位置。
那么问题来了, 滑动窗口的起始位置如何移动呢?
滑动窗口也可以理解为双指针法的一种!只不过这种解法更像是一个窗口的移动,所以叫做滑动窗口更适合一些。
这里还是以题目中的示例来举例,s=7, 数组是 2,3,1,2,4,3,来看一下查找的过程:
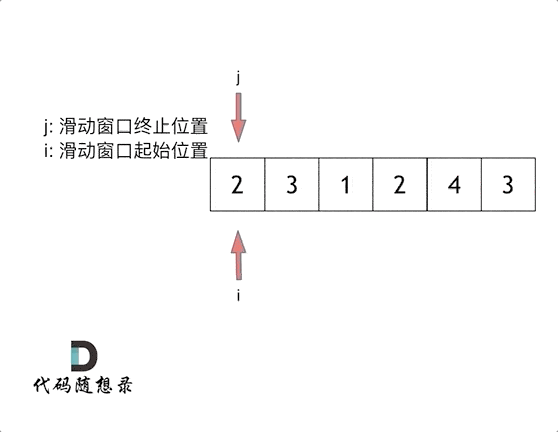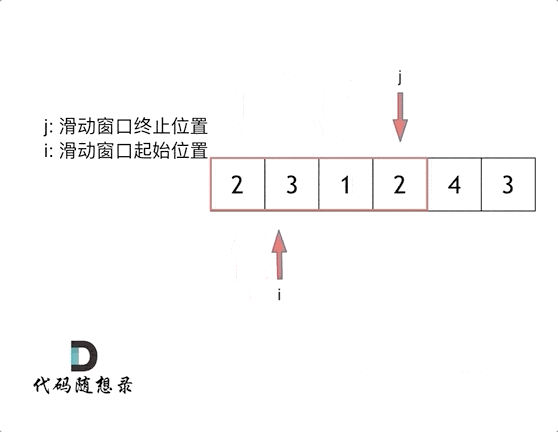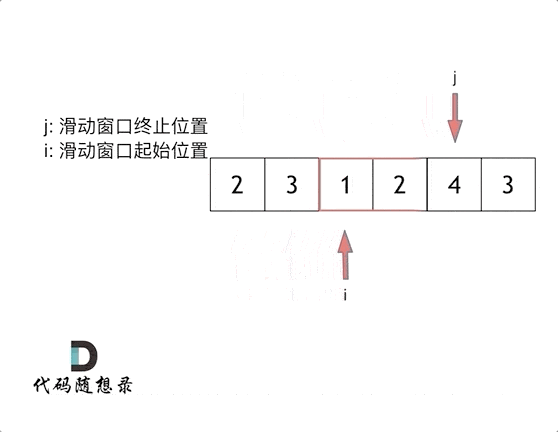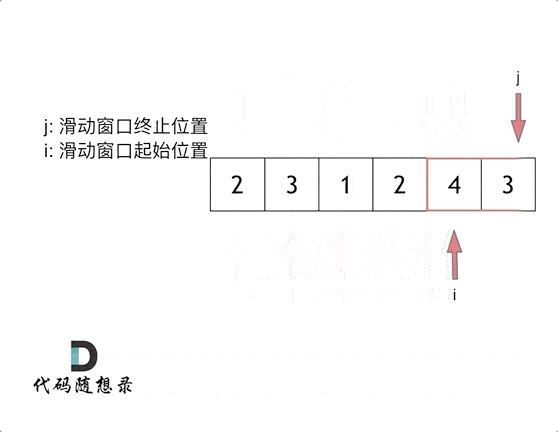
// 我思考的过程
function minSubArrayLen(target: number, nums: number[]): number {
let n = Infinity
let slowIndex = 0
let all = 0
for(let fastIndex = 0;fastIndex < nums.length; fastIndex++){
all += nums[fastIndex]
// 配合动画理解更好
if(all >= target){
n = Math.min(n, fastIndex - slowIndex + 1)
// all 将最后一个和第一个剪掉,slow向前,fast后退一个
all = all - nums[slowIndex] - nums[fastIndex]
fastIndex--
slowIndex++
}
}
return n === Infinity ? 0 : n
};
// 其实用while来移动左窗口更好
function minSubArrayLen(target: number, nums: number[]): number {
let n = Infinity
let slowIndex = 0
let all = 0
for(let fastIndex = 0;fastIndex < nums.length; fastIndex++){
all += nums[fastIndex]
while(all >= target){
n = Math.min(n, fastIndex - slowIndex + 1)
all = all - nums[slowIndex]
slowIndex++
}
}
return n === Infinity ? 0 : n
};
- 时间复杂度:O(n)
while 而不是 if因为使用 while 是为了 尽可能缩小窗口的大小,而 if 只能缩一次,不能连续缩。
类比一下 if 和 while 的区别:
- 用
if:
if (sum >= target) {
// 只缩一次
minLen = Math.min(minLen, right - left + 1)
sum -= nums[left]
left++
}
只判断了一次:如果这次 sum >= target,就缩一下。但可能缩一次还不够,还可以继续缩,得到更短的子数组。
while可以不断缩:
while (sum >= target) {
// 一直缩,直到 sum < target
minLen = Math.min(minLen, right - left + 1)
sum -= nums[left]
left++
}
只要总和还满足 sum >= target,我就不停地缩小窗口左边界,直到再缩就不满足为止。
螺旋矩阵
区间和
https://www.programmercarl.com/kamacoder/0058.%E5%8C%BA%E9%97%B4%E5%92%8C.html#%E6%80%9D%E8%B7%AF
https://kamacoder.com/problempage.php?pid=1070
思路
数组上常用的解题技巧:前缀和
代码
// 导入 readline 模块
const readline = require('readline');
// 创建 readline 接口实例
const rl = readline.createInterface({
input: process.stdin, // 从标准输入读取
output: process.stdout, // 输出到标准输出(主要用于提示,这里可以省略)
terminal: false // 表明这不是一个交互式终端
});
function main(){
let inputlines = []
rl.on("line", (line) => {
inputlines.push(line.trim())
})
rl.on("close", () => {
let length = Number(inputlines[0])
let arr = inputlines.slice(1, length + 1).map(item => Number(item))
let numArr = []
let n = 0
for (let i = 0; i < length; i++){
n += arr[i]
numArr[i] = n
}
let sumArr = inputlines.slice(length + 1, inputlines.length)
for (let i = 0; i < sumArr.length; i++){
let [a, b] = sumArr[i].split(' ').map(item => Number(item))
if (a === 0) {
console.log(numArr[b]);
} else {
console.log(numArr[b] - numArr[a - 1]);
}
}
})
}
main()
numArr[b] - numArr[a - 1]假设有一个数组 arr = [1, 2, 3, 4, 5],我们构建它的前缀和数组 prefixSum,如下:
复制编辑prefixSum[0] = arr[0] = 1
prefixSum[1] = arr[0] + arr[1] = 3
prefixSum[2] = arr[0] + arr[1] + arr[2] = 6
prefixSum[3] = arr[0] + arr[1] + arr[2] + arr[3] = 10
prefixSum[4] = arr[0] + arr[1] + arr[2] + arr[3] + arr[4] = 15
即:
arr = [1, 2, 3, 4, 5]
prefixSum = [1, 3, 6, 10, 15]
sum[a, b] = prefixSum[b] - prefixSum[a - 1]
例子:
- 区间
[1, 3]:2 + 3 + 4 = 9=>prefixSum[3] - prefixSum[0] = 10 - 1 = 9 - 区间
[0, 2]:1 + 2 + 3 = 6=>prefixSum[2] - prefixSum[-1]❌ 这不合法!
开发商购买土地
补充
ACM输入输出模式
// 导入 readline 模块
const readline = require('readline');
// 创建 readline 接口实例
const rl = readline.createInterface({
input: process.stdin, // 从标准输入读取
output: process.stdout, // 输出到标准输出(主要用于提示,这里可以省略)
terminal: false // 表明这不是一个交互式终端
});
function main(){
let inputlines = []
rl.on("line", (line) => {
inputlines.push(line.trim())
})
rl.on("close", () => {
// 输出输入的值,根据输入的值,来先获取的你所需要的参数
console.log(inputlines)
})
}
main()
举例
题目描述
给定一个整数数组 Array,请计算该数组在每个指定区间内元素的总和。
输入描述
第一行输入为整数数组 Array 的长度 n,接下来 n 行,每行一个整数,表示数组的元素。随后的输入为需要计算总和的区间下标:a,b (b > = a),直至文件结束。
输出描述
输出每个指定区间内元素的总和。
输入示例
5
1
2
3
4
5
0 1
1 3输出示例
3
9
// 导入 readline 模块
const readline = require('readline');
// 创建 readline 接口实例
const rl = readline.createInterface({
input: process.stdin, // 从标准输入读取
output: process.stdout, // 输出到标准输出(主要用于提示,这里可以省略)
terminal: false // 表明这不是一个交互式终端
});
function main(){
let inputlines = []
rl.on("line", (line) => {
inputlines.push(line.trim())
})
rl.on("close", () => {
// 数组长度
const length = Number(inputlines[0])
// 拿到数组
const arr = inputlines.slice(1, length + 1).map(item => Number(item))
// 拿到需要计算的数组
const sumArr = inputlines.slice(length + 1, inputlines.length)
for (let i = 0; i < sumArr.length; i++){
const [a, b] = sumArr[i].split(' ').map(item => Number(item))
// 开始计算(当然这里可以这么做但不是最好的)
// 开始计算
const newArr = arr.slice(a, b + 1)
let n = 0
for (const item of newArr) {
n += item
}
// 最后的结果console.log 即可
console.log(n)
}
})
}
main()